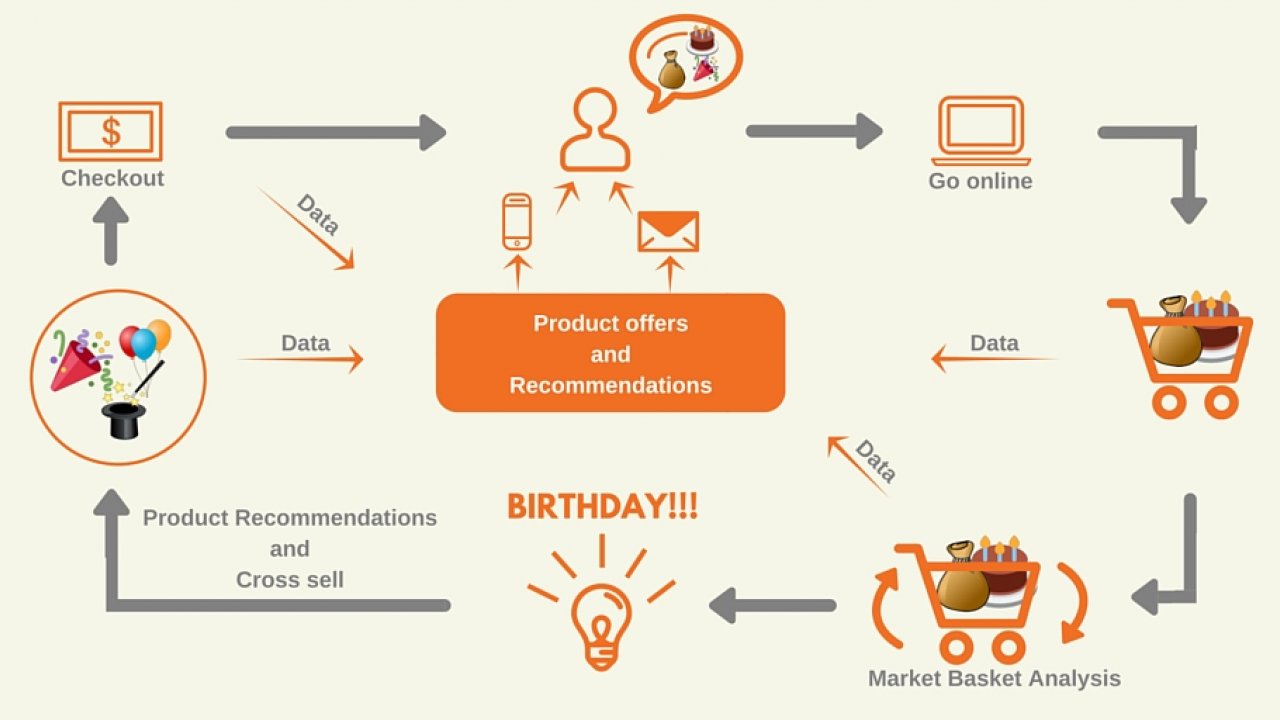
ANALYTICS IN HEALTHCARE
Traditionally, healthcare has always used statistical analyses in clinical research. However, with the recent massive explosion of structured and unstructured data from the digitization of patients’ health records (EHR), hospital inpatient claims data, machine generated/sensor data, analytics has become essential to enhance functionalities across multiple sectors in healthcare including public health management, hospital administration, personalized medicine and medical imaging.

With EHR data, predictive analytics can help providers treat patients based on their past behaviours to mitigate future events, such as a diabetic ending up in the emergency room because he did not refill his medication or a child with asthma requiring a hospital admission due to environmental triggers of her disease. For e.g., in an effort to lower the rate of veteran suicides, the US army is conducting a study (Army STARR) to leverage a predictive risk model2 to identify patients who may be likely to harm themselves.Previous models used to mine the EHR data to identify patients at risk of self-harm by flagging past attempts at suicide. STARR, however, narrowed down more than 400 personal traits into a smaller set of factors that were consistently predictive of suicidal behaviour using machine learning algorithms. It then assigned a risk score using the relevant clinical data points such as prescription drug use, behavioural history, military experience, access to weaponry, age at enlistment, past conflicts with leadership, and IQ scores.

Public health management: Analytics can be used to prevent bottlenecks in supply and demand in the overall access to care. For example, University of Florida leveraged Google Maps and free public health data to identify factors of demand for medical facilities (e.g. population growth, chronic disease rates) in municipalities and compared those factors to the availability of medical services in those areas. The university located three Florida counties that were underserved for breast cancer screening and redirected its mobile care units accordingly.

Combining historical medical literature, google maps, geographical and socio economic conditions and free public health data, hot spots for disease outbreaks can be identified and contained. Let’s take the research which was jointly conducted by IBM with John Hopkins University and University of California at San Francisco 5 as an example. Merging information on changes in rainfall, temperature, soil acidity to gauge the population of wild animals and insects of a particular geography with other public data like transportation and airport and highway traffic they were able to establish a pattern in dengue and malaria outbreaks in the states of Texas and Florida.
Another method to track outbreaks can be disease networking. Use of big data analytics to study the timing and location of search engine queries, consumers’ posts on social networks to predict disease outbreaks can potentially support key prevention programs such as disease surveillance and outbreak management. Case in point, Researchers at the Johns Hopkins School of Medicine used data from Google Flu Trends to predict sudden increases in flu related emergency room visits at least a week before warnings from the CDC.6 Likewise, using social media analytics on Twitter updates to track the spread of cholera in Haiti after the January 2010 earthquake was as accurate as (and two weeks ahead of) official reports.

Analytics used in hospital administration: A major difficulty for hospitals is to provide interventions and care such that patients’ readmission rates are reduced. A hospital readmission is when a patient who had been discharged from a hospital is admitted again to that hospital or another hospital within a specified time frame. Time frames can differ across studies with the most common being 30-day, 90-day, and 1-year readmissions. Avoidable readmissions mainly occur because the patient’s initial problem remains unresolved or because of the patient’s mismanagement/ misunderstanding of their condition. Leveraging EHR and socioeconomic data derived factors (e.g. patient’s current length of stay, acuity of admission, number of ED visits in the previous six months, functional status, discharge hospital ward, housing discontinuities, drug use), classification algorithms like random forests, SVM are used to create a risk readmission scorecard. Each patient who is admitted is assigned a risk score on the basis of which healthcare providers implement timely interventions to reduce the number of the patient’s visits to the hospital.

Personalized/precision medicine: It involves using patients’ individual characteristics (e.g. genome sequence, microbiome composition, health history, lifestyle, diet, environments) to enable health care providers to tailor treatment and prevention strategies for each patient. It requires the ability to classify individuals into subpopulations that differ in their susceptibility to a particular disease, the morphology of the disease or in their response to a specific treatment. This can be achieved by using panomics (molecular biology techniques like genomics, proteomics) and systems biology9 to analyse the cause of an individual patient’s disease at the molecular level and then use targeted therapy to address that individual patient’s disease progress. The patient’s response is then tracked closely and the treatment finely adapted to the patient’s response.
Thus, insight into disease mechanisms is necessary to developing targeted therapies. A major goal in genomic research is to predict phenotypes (traits of an organism influenced by interaction of its genes with its environment) from a genotype (inherited instructions it carries within its genome) as phenotypes are studied to understand disease risks.

Yet even within a single cell, the genome directs the state of the cell through many layers of intricate and interconnected biophysical processes and control mechanisms. Analysing just the genotypes to infer results on phenotypes does not give sufficient information on the disease mechanisms. As a result, the subsequent targeted therapies may not be effective. It can be counteracted by training a supervised machine learning algorithm (e.g. neural networks) to predict measurable intermediate molecular functions (e.g. the distribution of proteins along a transcript, concentration of proteins) which can then be linked to phenotypes.
Medical imaging uses learning algorithms to analyse data contained within medical images to detect distinct patterns. Given a collection of images, dimensionality reduction and feature extraction techniques are applied to derive relevant biomarkers (colour layout, edge histogram, colour edge direction and colour texture). The biomarkers are then weighted by classifier algorithms (e.g. SVM classifier) to detect patterns/anomalies. The updated images are further reviewed by diagnosticians and the feature weights in the classifier algorithms are trained accordingly for subsequent iterations. However, image analytics can be further used to assist physicians in reducing varying subjective interpretation and human error, thereby accelerating the process of treatment and recovery. For e.g.,11 researchers in China have found that their machine-learning computations separate malignant from benign properties more accurately than an inexperienced radiologist—but not as accurately as the experienced radiologist whose know-how was used to create the algorithms.

Two radiologists reviewed ultrasound images of 970 histopathologically proven thyroid nodules in 970 patients and their findings were compared with machine-building algorithms: the Naïve Bayes classifier, the support vector machine, and the radial basis neural function network. The results showed the experienced radiologist of 17 years achieved the highest predictive accuracy of 88.7% with a specificity of 85.3%, whereas the radial basis function (RBF)–neural network (NN) achieved the highest sensitivity of 92.3%. However, the algorithms were more accurate than the inexperienced radiologist, who had only 3 years’ similar experience.