CASINOS & EVOLVING ANA...
Analytics are used by companies to be more competitive and the financial services industry has known this for decades. In fact, many financial services analytics professionals are moving to gaming as both industries need to balance risks and returns. More and more, casinos are using analytics to make decisions in areas that have traditionally relied upon “expertise” rather than data-driven approaches to increase profits…
Where to strategically place games on the casino floor

Today, modeling teams at a number of casinos use software such as SAS to predict the impact of moving games from one area of a casino floor to another1.
To set a baseline, data is collected on how much money each game, whether table games or slots, currently brings in as well as how people move about the casino. When the gathered data is combined with the odds of a particular game paying out, the analytics team can model what the performance would look like in different locations to help determine where the game should be placed in order to achieve the optimal performance level. This is a similar technique used by supermarket companies. Just as with a grocery store, where on the casino floor would you get the best yield?
A holistic data-driven approach for all casino operations

Gaming revenue is not the largest portion of what casinos bring in. They derive much of their revenue from their resort operations. For example, a good way to encourage gambling is to give customers free nights or discounted dinners in the hotel that houses a casino. But the casino would lose money if it did so for everyone, because some people don’t gamble much. To help pinpoint such offers, savvy Casinos run customer analytics applications on data it has collected showing how often individual guests gamble, how much money they tend to spend in the casino and what kinds of games they like. This is all part of a significant shift in how casinos do business where it’s getting to the point that casinos are being run like financial services firms.
The challenges of shifting to Big Data

At MGM Resorts’ 15 casinos across the United States, thousands of visitors are banging away at 25,000 slot machines. Those visitors rang up nearly 28 percent of the company’s $6 billion in annual domestic revenue in 2013. Using the game and customer data that MGM collects daily and the behind-the-scenes software that transforms the data into critical insights, in turn, boost the customer experience and profit margins2.
Lon O’Donnell, MGM’s first-ever director of corporate slot analytics, is challenged to show why big data is a big deal when it comes to plotting MGM’s growth. “Our goal is to make that data more digestible and easier to filter,” says O’Donnell, who estimates that Excel still handles an incredible 80 percent of the company’s workload. In the near term, that means the team is experimenting with data visualization tools (Slotfocus dashboard - right) to make slot data more crunchable. Heavy-lifting analytics are a goal down the road3. MGM isn’t the only gaming company interested in big data - nor was it the first. That distinction goes to Gary Loveman, who left teaching at Harvard Business School for Las Vegas in the late 1990s and turned Harrah’s into gaming’s first technology-centric player.
History has caught up with the industry. For decades, Las Vegas casinos were some of the only legal gambling outfits in the country, so they could afford to be complacent. That advantage disappeared during the past two decades with the rise of legal gambling in 48 states. The switch to slicker, more sophisticated cloud apps is still on the horizon. One reason why is the regulatory nature of gaming: Casinos tend to organize data in spreadsheets to report to regulators, who review the accounting and verify that slots perform within legal specifications. But those reports are not ideal business intelligence sources.
Using Big Data to catch cheaters

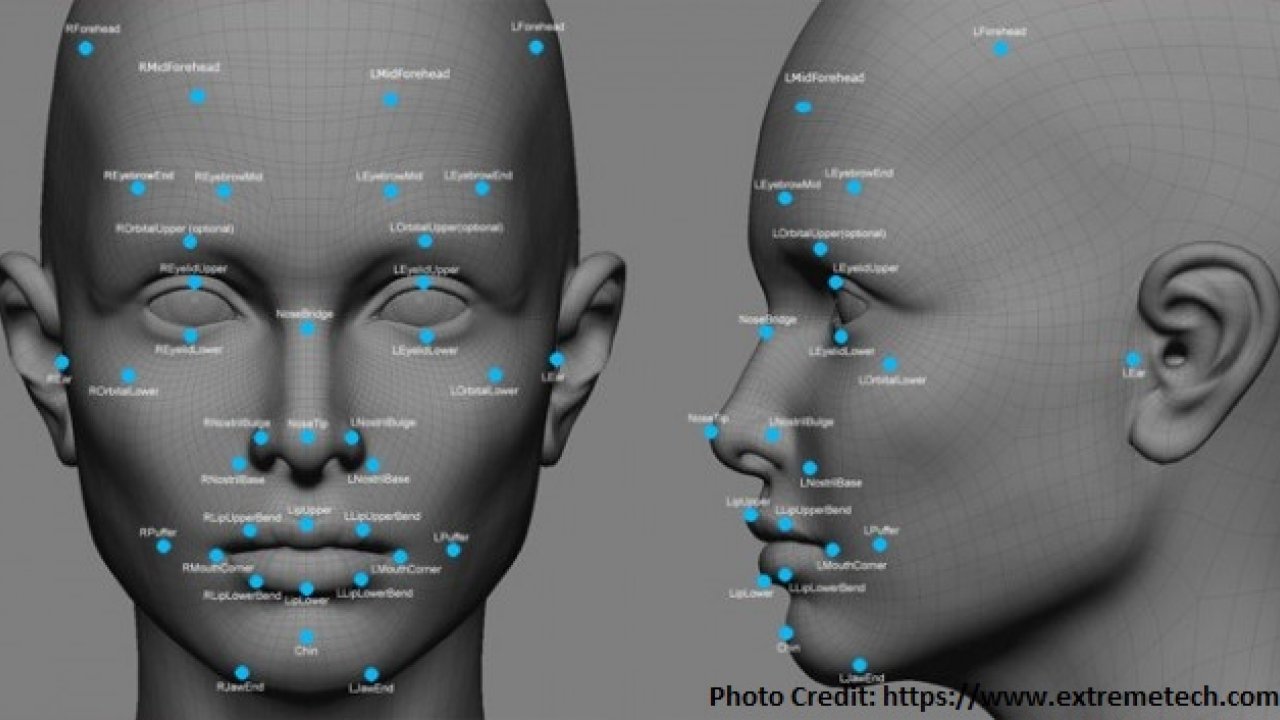
Casinos are at the forefront of new tools to help them make more money and reduce what they consider to be fraud. One tool is something called non-obvious relationship awareness (NORA) software that allows casinos to determine quickly if a potentially colluding player and dealer have ever shared a phone number or a room at the casino hotel, or lived at the same address4,5. “We created the software for the gaming industry,” says Jeff Jonas, founder of Systems Research & Development, which originally designed NORA. The technology has proved so effective that Homeland Security adapted it to sniff out connections between suspected terrorists. “Now it’s used as business intelligence for banks, insurance companies and retailers,” Jonas says. The image above shows three types of cameras feed the video wall in the Mirage’s surveillance room (top-right): Fixed-field-of-view units focus on tables; motorized pan-tilt-zoom cameras survey the floor; and 360-degree cams take in an entire area.
Big Data and attendant technologies are starting to transform businesses right before our very eyes. Old ways of doing things are beginning to fall by the wayside. When specific examples like NORA become more public, Big Data suddenly becomes less abstract to those who make decisions.
Analytics are used by companies to be more competitive and the financial services industry has known this for decades. In fact, many financial services analytics professionals are moving to gaming as both industries need to balance risks and returns. More and more, casinos are using analytics to make decisions in areas that have traditionally relied upon “expertise” rather than data-driven approaches to increase profits…
Where to strategically place games on the casino floor

Today, modeling teams at a number of casinos use software such as SAS to predict the impact of moving games from one area of a casino floor to another1.
To set a baseline, data is collected on how much money each game, whether table games or slots, currently brings in as well as how people move about the casino. When the gathered data is combined with the odds of a particular game paying out, the analytics team can model what the performance would look like in different locations to help determine where the game should be placed in order to achieve the optimal performance level. This is a similar technique used by supermarket companies. Just as with a grocery store, where on the casino floor would you get the best yield?
A holistic data-driven approach for all casino operations

Gaming revenue is not the largest portion of what casinos bring in. They derive much of their revenue from their resort operations. For example, a good way to encourage gambling is to give customers free nights or discounted dinners in the hotel that houses a casino. But the casino would lose money if it did so for everyone, because some people don’t gamble much. To help pinpoint such offers, savvy Casinos run customer analytics applications on data it has collected showing how often individual guests gamble, how much money they tend to spend in the casino and what kinds of games they like. This is all part of a significant shift in how casinos do business where it’s getting to the point that casinos are being run like financial services firms.
The challenges of shifting to Big Data

At MGM Resorts’ 15 casinos across the United States, thousands of visitors are banging away at 25,000 slot machines. Those visitors rang up nearly 28 percent of the company’s $6 billion in annual domestic revenue in 2013. Using the game and customer data that MGM collects daily and the behind-the-scenes software that transforms the data into critical insights, in turn, boost the customer experience and profit margins2.
Lon O’Donnell, MGM’s first-ever director of corporate slot analytics, is challenged to show why big data is a big deal when it comes to plotting MGM’s growth. “Our goal is to make that data more digestible and easier to filter,” says O’Donnell, who estimates that Excel still handles an incredible 80 percent of the company’s workload. In the near term, that means the team is experimenting with data visualization tools (Slotfocus dashboard - right) to make slot data more crunchable. Heavy-lifting analytics are a goal down the road3. MGM isn’t the only gaming company interested in big data - nor was it the first. That distinction goes to Gary Loveman, who left teaching at Harvard Business School for Las Vegas in the late 1990s and turned Harrah’s into gaming’s first technology-centric player.
History has caught up with the industry. For decades, Las Vegas casinos were some of the only legal gambling outfits in the country, so they could afford to be complacent. That advantage disappeared during the past two decades with the rise of legal gambling in 48 states. The switch to slicker, more sophisticated cloud apps is still on the horizon. One reason why is the regulatory nature of gaming: Casinos tend to organize data in spreadsheets to report to regulators, who review the accounting and verify that slots perform within legal specifications. But those reports are not ideal business intelligence sources.
Using Big Data to catch cheaters

Casinos are at the forefront of new tools to help them make more money and reduce what they consider to be fraud. One tool is something called non-obvious relationship awareness (NORA) software that allows casinos to determine quickly if a potentially colluding player and dealer have ever shared a phone number or a room at the casino hotel, or lived at the same address4,5. “We created the software for the gaming industry,” says Jeff Jonas, founder of Systems Research & Development, which originally designed NORA. The technology has proved so effective that Homeland Security adapted it to sniff out connections between suspected terrorists. “Now it’s used as business intelligence for banks, insurance companies and retailers,” Jonas says. The image above shows three types of cameras feed the video wall in the Mirage’s surveillance room (top-right): Fixed-field-of-view units focus on tables; motorized pan-tilt-zoom cameras survey the floor; and 360-degree cams take in an entire area.
Big Data and attendant technologies are starting to transform businesses right before our very eyes. Old ways of doing things are beginning to fall by the wayside. When specific examples like NORA become more public, Big Data suddenly becomes less abstract to those who make decisions.